기자단 기사

안녕하세요 임은규 기자입니다.

허수와 오일러의 등식을 설명해보겠습니다.

복소평면에서 1을 2/ㅠ만큼 반시계 방향으로 이동하면 i다.

(이것은 복소평면을 소재로 한 개념이며, 현실적으로는 i가 아니다.)

(허수 i의 정의는 저번 글을 참고)

왜 그럴까?

그것은 원을 그리고 그 안의 복소평면 (허수축과 실수축이 있는 평면 (전글에 나와 있음))에 그려 보면 된다.

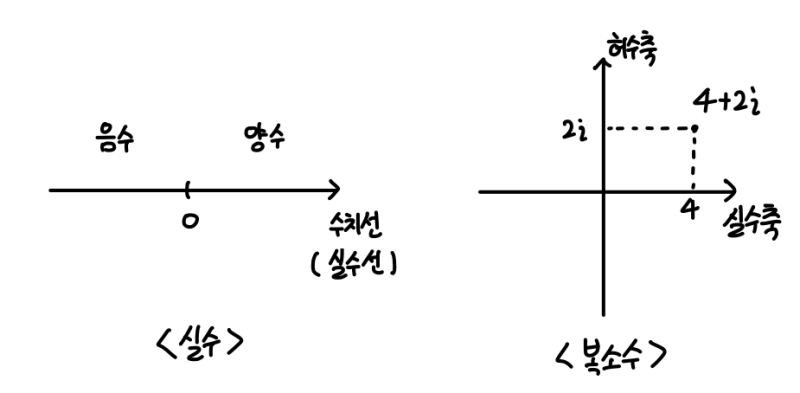
(출처: https://m.blog.naver.com/bshte1440/222448308715)

자. 복소평면을 알아야지 설명을 들을 수 있다.

오른쪽 부분은 +이고 왼쪽 부분은 -이다.

그러면 +에서 -까지 걸리는 거리는 원의 반이니 ㅠ이다.

• 원주율: 지름을 1로 했을 때 원의 둘레의 비율로 약 3.1415926535897932384626433832795028….이다. 편의상 3.14로 부르며, 2로 나누면 약 1.57이다. 그런데 그게 중요한 것은 아니다.

실수축에서 반지름이 1인 원을 그린다고 가정해보자.

그대로 약 1.57만큼 원을 따라 가면 허수축,즉 i축이 나온다. (허수축 바로 위에서 멈춘다.)

이제 2/ㅠ만큼 이동하면 왜 i인지 알 수 있을 것이다.

그러면 이제 오일러 등식을 이해해 보자.

(e는 나중에 자세히 설명하겠다. )

오일러 등식은 아래와 같다.

(출처:​​http://plug.hani.co.kr/futures/1673339)

그냥 e의 i제곱이 무엇인지 알아보겠다.

e의 i제곱은 한 번 1만큼 돌린 것이다. 그러면 e의 2i제곱은 두번 1만큼 돌린 것이다.그러니까 e의 파이 i제곱은 파이까지 갔으니 +1의 반대쪽, 즉 -1이 된다.

그러므로 당연하게 1을 더하면 0이다.

ㅠ와 i에 관한 설명은 끝내고 제곱해서 i가 되는 수에 대해 설명하겠다.(i루트)

제곱해서 i가 되는 수는 제곱해서 90도가 되는 수니 45도다. 복소수로 나타내면(약 0.75니 0.75로 표기)

(a(실수축(0.75))+b(허수축(0.75)i이다.

보통 제곱해서 허수가 되는 수가 없다고 하는데( 나도 그렇게 들었다.)

그 이유는 허수는 실체가 없다고 생각하기 때문이다.

하지만 음수도 실체가 없지만 제곱해서 음수가 되는 수가 있지 않는가?

이 방법을 이용해서 세제곱해서 i가 되는 수는 30도이다.(i루트 루트)(복소수로 나타내면 0.75+0.25i)

이 방법을 응용하면 네제곱해서 i가 되는 수(i루트 루트 루트), 다섯제곱해서 i가 되는 수도 구할 수 있다.(i루트 루트 루트 루트)

허수 i에 관한 글이었다.

이상으로 이 글을 마치겠습니다!